강의 초반부에서는 트리에 대한 기본적인 설명을 해주었다.
특히 적어둘 만한 것으로는 이진 트리에 관한 내용이 있었다. 학교 수업에서 배웠으나 잊고 있었던 내용인데, 이 기회에 확실히 기억해둬야겠다.
포화, 완전 이진 트리의 인덱스
포화 이진 트리와 완전 이진 트리는 그 정의로 인해 반드시 인덱스가 특정한 규칙을 띤다.
루트의 인덱스를 1로 하고 각 레벨의 왼쪽부터 차례대로 번호를 매기면 각 노드의 인덱스는 다음의 그림과 같이 된다.

이때 요소들은 반드시 다음의 규칙을 따른다.
부모의 인덱스를 i라 할 때,
왼쪽 자식의 인덱스는 2i 이고
오른쪽 자식의 인덱스는 2i+1 이다.
이진 트리의 순회법
이진 트리의 순회법에는 3가지가 있다.
- 전위 순회(Preorder) : 루트 - 왼쪽 서브트리 - 오른쪽 서브트리
- 중위 순회(Inorder) : 왼쪽 - 루트 서브트리 - 오른쪽 서브트리
- 후위 순회(Postorder) : 왼쪽 - 오른쪽 서브트리 - 루트 서브트리
루트의 방문 순번에 따라 이름이 정해졌다고 보면 편하다.
예를 들면 다음과 같다.

이러한 이진 트리가 있다.
이 이진 트리를 세 가지 방법으로 순회해볼 것이다.
1. 전위 순회
먼저 전위 순회를 해 보자.
전위 순회는
루트 - 왼쪽 - 오른쪽이다.

전체 트리의 입장에서 루트인 1부터 방문한다.
1
그 다음은 왼쪽 서브트리를 정복해야 한다.
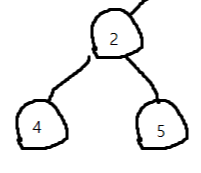
왼쪽 서브트리 내에서 전위 순회를 한다. 이 서브트리 입장에서 루트인 2를 가장 먼저 방문하고, 그 다음으로 왼쪽인 4, 마지막으로 오른쪽인 5를 방문한다.
1 - 2 - 4 - 5

1, 2, 4, 5 를 방문했으니 전체 트리의 입장에서 루트와 왼쪽 서브트리 방문이 끝났다. 이제 오른쪽 서브트리 차례이다.
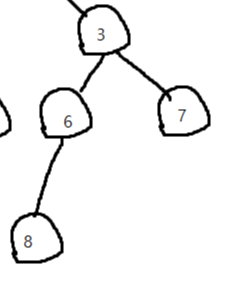
일단 이 서브트리 입장에서 루트는 3이다. 3부터 방문한다.
1 - 2 - 4 - 5 - 3
그 다음 왼쪽 서브트리로 들어간다.

전위 순회이므로 루트인 6을 먼저 방문하고 왼쪽의 8을 방문한다.
1 - 2 - 4 - 5 - 3 - 6 - 8

이 트리의 입장에서 3(루트)와 왼쪽 서브트리(6과 8)을 모두 방문한 상태가 되었다. 이제 오른쪽 차례이다. 7을 방문해준다.
1 - 2 - 4 - 5 - 3 - 6 - 8 - 7

모든 노드의 방문이 끝났다.
전위 순회로 이 트리를 순회할 경우 방문 순서는 다음과 같다.
1 - 2 - 4 - 5 - 3 - 6 - 8 - 7
2. 중위 순회
다음으로 중위 순회를 해보자.
중위 순회는
왼쪽 - 루트 - 오른쪽이다.

먼저 왼쪽 서브트리부터 정복해야 한다.

이 서브트리 입장에서 왼쪽에는 4밖에 없다. 4를 가장 먼저 방문한다.
그 다음 이 서브트리 입장에서 루트인 2를 방문한다.
마지막으로 5를 방문하면 이 서브트리는 방문이 끝난다.
4 - 2 - 5

전체 트리 입장에서 왼쪽의 방문이 끝났으니 루트인 1을 방문해준다.
4 - 2 - 5 - 1
그 다음은 오른쪽 서브트리 차례이다.

이 서브트리 입장에서 왼쪽 서브트리인 부분부터 방문해주어야 한다. 왼쪽은 6과 8로 이루어진 서브트리이다.

중위 순회이므로 왼쪽인 8부터 방문하고 그 다음 6을 방문해준다.
4 - 2 - 5 - 1 - 8 - 6

이 서브트리 입장에서 왼쪽 서브트리의 방문이 모두 끝났으니,
루트인 3을 방문해준다.
그 다음 오른쪽인 7을 방문해준다.
4 - 2 - 5 - 1 - 8 - 6 - 3 - 7

모든 노드의 방문이 끝났다.
전위 순회로 이 트리를 순회할 경우 방문 순서는 다음과 같다.
4 - 2 - 5 - 1 - 8 - 6 - 3 - 7
3. 후위 순회
마지막으로 후위 순회를 해보자.
후위 순회는
왼쪽 - 오른쪽 - 루트이다.

전체 트리의 입장에서 왼쪽 서브트리인 부분부터 방문해야 한다.

이 서브트리 안에서 후위 순회를 한다.
일단 왼쪽인 4를 방문하고, 그 다음은 오른쪽인 5를 방문한 뒤, 마지막으로 루트인 2를 방문한다.
4 - 5 - 2

왼쪽 서브트리의 방문이 모두 끝났으니 그 다음은 오른쪽 서브트리 차례이다.

이 서브트리 입장에서 왼쪽 서브트리인 부분부터 방문해야 한다.

여기서 왼쪽인 8을 먼저 방문하고, 오른쪽은 아무것도 없으니 바로 루트인 6을 방문해준다.
4 - 5 - 2 - 8 - 6

왼쪽 서브트리 방문이 끝났으니 그 다음은 오른쪽인 7을 방문한다.
그리고 루트인 3을 방문해준다.
4 - 5 - 2 - 8 - 6 - 7 - 3

전체 트리의 루트인 1만 빼놓고 왼쪽과 오른쪽 서브트리를 모두 방문했다.
마지막으로 1을 방문해주면 순회가 끝난다.
4 - 5 - 2 - 8 - 6 - 7 - 3 - 1
우선순위 큐란?
그 다음으로는 우선순위 큐에 대한 내용이 이어졌다.
우선순위 큐는 입력 순서에 상관 없이 우선순위가 높은 자료가 먼저 꺼내지는 자료구조이다.
필수 기능은 다음의 세 가지가 있다.
- Top : 가장 우선순위가 높은 원소를 리턴한다.
- Push : 우선순위 큐에 원소를 하나 추가한다. (넣기)
- Pop : Top에 있는 원소를 제거한다. (빼기)
Heap
우선순위 큐를 구현하는 방법에는 여러 가지가 있으나, 강의에서는 특히 힙(Heap)을 사용한 구현법을 다루었다.
Heap은 부분적으로 정렬된 완전 이진 트리로, 만족해야 하는 조건이 딱 하나 있다. 그것은 부모의 우선순위가 자식들의 우선순위보다 반드시 높아야 한다는 것이다. 레벨이 동일한 자식들끼리는 우선순위가 섞여있어도 상관없다.
Heap을 사용한 Push(삽입, Insertion)와 Pop(삭제, Deletion)의 과정은 다음과 같다.
1. 삽입
삽입은, 일단 새 노드를 제일 끝자리에 넣어둔 다음 그 노드의 자리를 옮겨가며 알맞는 곳에 가져다놓는 방식으로 이루어진다.
- Heap의 가장 뒷 순서, 즉 마지막 원소의 다음 위치에 일단 넣는다.
- 새로 들어간 노드의 부모를 살핀다. 부모의 우선순위가 새 노드보다 낮다면 부모와 새 노드의 자리를 서로 바꾼다. 부모의 우선순위가 새 노드보다 더 높다면 더이상 자리를 바꿀 필요가 없으므로 삽입 과정은 여기서 끝난다.
- 새 노드의 부모가 새 노드보다 우선순위가 높거나, 혹은 새 노드가 루트 자리에 올라갈 때까지 2의 과정을 반복한다.
2. 삭제
삭제도 삽입과 비슷한 방식으로 하면 되는데, 삽입에서 새 노드가 leaf부터 root의 방향으로 한 자리씩 이동했다면 여기서는 반대로 특정 노드가 root부터 시작하여 점점 아래쪽으로 이동한다.
- 우선순위가 가장 높은 원소부터 취한다는 우선순위 큐의 특성상, 삭제는 반드시 우선순위가 가장 높은 노드인 root에 대하여 이루어진다. 따라서 root의 원소를 없애주어야 하는데, root를 그냥 null로 비워놔버리면 정렬이 번거로워진다. 그 대신, 비어버린 root 자리에 가장 우선순위가 낮은 노드를 넣는다. 이렇게 root 자리에 들어온 노드를 편의상 A라고 부르겠다.
- 이제 A를 아래로 한 자리씩 이동시켜주며 제자리를 찾아주면 된다. 제일 우선순위가 낮은 놈이 root 자리에 올라왔으니 A의 왼쪽과 오른쪽 직속 자식들은 A보다 우선순위가 높거나 같다. 두 자식 중 A보다 우선순위가 높은 놈이 있다면, 왼쪽과 오른쪽 중 더 우선순위가 높은 자식을 골라 A와 자리를 서로 바꾼다.
- A의 양쪽 자식이 모두 A보다 우선순위가 낮거나 같은 상황이 되거나, 혹은 A가 leaf까지 내려갈 때까지 2의 과정을 반복한다.
Heap의 시간복잡도
Heap을 이용한 우선순위 큐의 세 가지 연산 Top, Push, Pop의 시간복잡도는 다음과 같다.
일단 Top 연산의 경우 그냥 root의 값을 리턴하기만 하면 되므로 상수 시간이 걸린다.
이진 트리의 특성상 원소의 개수가 N개라고 할 때 트리의 높이는 $log_2 N$(이하 $log N$)이다. Push와 Pop의 시간복잡도는 이 점을 이용해 쉽게 알아낼 수 있다.
Push(삽입)을 할 때, 최악의 경우에 새 노드는 leaf부터 root까지 올라가게 된다. 이 과정에서 최대 $log N$번의 값 비교와 이동이 발생한다.
Pop(삭제)도 비슷하다. 최악의 경우의 노드 A는 root부터 leaf까지 이동하는데, 이 과정에서 최대 $log N$번의 값 비교와 이동 과정을 거친다.
결과적으로 Top은 O(1), Push와 Pop은 O($log N$)의 시간복잡도를 가진다.
선형 자료구조를 이용해 우선순위 큐를 구현했을 때보다 훨씬 효율적이다.
아래는 지금까지의 내용을 참고하여 우선순위 큐를 구현해본 결과이다.
자바에서 1차원 배열을 활용한 우선순위 큐 구현하기
2022 상반기 신촌 ICPC 알고리즘 캠프의 트리 강의 내용을 기반으로, 매우 기본적인 우선순위 큐 프로그램을 구현하였다. 우선순위 큐의 작동 방식을 제대로 이해하기 위하여 만들어보았다. 아무
blowupmomo.tistory.com
'기타 공부 > 2022 상반기 신촌 ICPC 알고리즘 캠프 노트정리' 카테고리의 다른 글
| 초급 8회차 그래프 탐색 (0) | 2022.06.01 |
|---|---|
| 초급 7회차 이분탐색 & 분할정복 (0) | 2022.05.18 |
| 초급 6회차 완전탐색과 백트래킹 (0) | 2022.04.05 |
| 초급 5회차 선형 자료구조 (0) | 2022.04.05 |
| 초급 4회차 그리디 알고리즘 (0) | 2022.04.04 |